[Random Musings] Misconceptions in Probability

Hey y'all.

For the last few days, I've seen some students struggling with conditional probability on the IB server. This isn't news or anything; conditional probabilities are usually poorly done overall, especially the SL folks. This post summarises what commonly show up on examiners' reports and how you can avoid it.

The concept of probability in IB is ENORMOUS, so I'll just focus on basic probability and combined probability. A solid foundation in this would ensure a good shot at solving the more complex, massive-tree-diagram-wordy-thingy questions.

Basics of probability

(1) giving answers which were greater than 1

You've probably heard of this statement 283187 times, but it's surprising the number of students who "innocently" report a probability of 2.0 due to a calculation error when dealing with decimals.

Honestly. If y'all ever report a probability greater than 1, I'd leave the room and SCREAM because you didn't pay attention to anything.

(2) thinking that outcomes are always equally likely

This is another massive misconception, and there are many ways to show that this isn't true. 

Case in point: get yourself a bag of marbles with 9 blue marbles and 1 red marble. Take one marble from the bag, record the colour then return the marble. Rinse and repeat until you have 5 colours recorded. There's a good chance you wouldn't get a SINGLE red in your list.

Just because there are two colours of marbles doesn't mean the probability of drawing each marble is equal.

(3) mixing up complementary events, mutually exclusive events and independent events

Let's roll a die. I'm positive that y'all have at least one (1) die in your house, otherwise, go buy one. Might help with your MCQ exams. :P

These three are usually muddled up, for a good reason: there are subtleties in the wording of these terms.

Complementary events: A and not A are complementary; the two outcomes cover the entire sample space.

Mutually exclusive events: either A or B can happen at any given time, not both. They might not cover the entire sample space.

Going back to our example, 

• '1' and 'not 1' are complementary events - they are the only two possible outcomes
• '1' and '2' are mutually exclusive but NOT complementary - there exists other outcomes, notably '3', '4', '5' and '6'

Independent events: now we're talkin different events happening and whether the occurence of one event affects the other. Not the outcomes of the same event as in complementary and mutually exclusive events; now we're interested in the relationship BETWEEN events.

Using our example, getting a '1' on the first roll and getting a '2' on the second roll are INDEPENDENT because the probability is "reset" after each roll and the results of the first roll do not affect the second roll.

An example of dependent events: if you roll a '1' or '2' on the first roll, you can now toss a coin. Now we have different outcomes depending on your first roll:

• if the first roll is 1 or 2, our outcome is 1H, 1T, 2H and 2T (H = heads and T = tails)
• if the first roll is neither 1 nor 2 (3, 4, 5 or 6), our outcome is 3, 4, 5 and 6.

(4) unable to list systematically and include all possibilities

In many probability questions, there are several ways to get to the same outcome and you must take everything into consideration. Be systematic or you risk missing or double-counting cases!

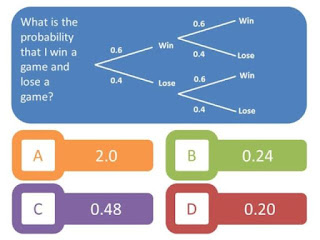
Consider this question, taken from Diagnostic Questions (now known as Eedi): 

(the original link with Craig Barton's discussion can be found here.)

There are two ways to win a game and lose a game:

• win the first and lose the second (P = 0.6 x 0.4)
• lose the first and win the second (P = 0.4 x 0.6)

This simple question shows how easy it is to miss a case if you rush through the question.

Alright y'all, it's been a long ride and y'all are probably sick of me right now.

I'll come back with a sequel on conditional probability when I'm in the mood to write more.

Enjoy the week!

Andrew

Source: questions and images from here.