[Advice Column] What makes a question hard?
Hello hoomans.
My long-time readers may have noticed that I tend to take
all of us on a tangent every so often. And today happens to be one of those
days.
If you hang out with me on the IB Discord server this is not
the first time I babble on designing and writing examinations. You know how
happy I am to talk about these nerdy things. I wrote two posts on how I write
exams, which you could find here and here. Today we’ll take a
crucial aspect – question difficulty – and dive deeper into what makes up the
difficulty of a question.
This is my attempt to distill some of the research I’ve read
in a more user-friendly, digestible way.
Perhaps not the most accurate but hopefully they serve as a
checklist for question writers to be cognizant of when they’re writing
questions for a mock exam.
Note that this does NOT apply to formative assessments;
the purpose is different and therefore you shouldn’t apply what’s written here
word by word. And if you’re not teaching maths (or science), I don’t think such
principles would apply.
After reading a handful of papers, both research papers and
documents from exam boards, there are three main factors that influence
the difficulty of the question. In assessment literature, sometimes you’ll
encounter the word “demand” instead of difficulty; 99% of the time you can
safely use them interchangeably.
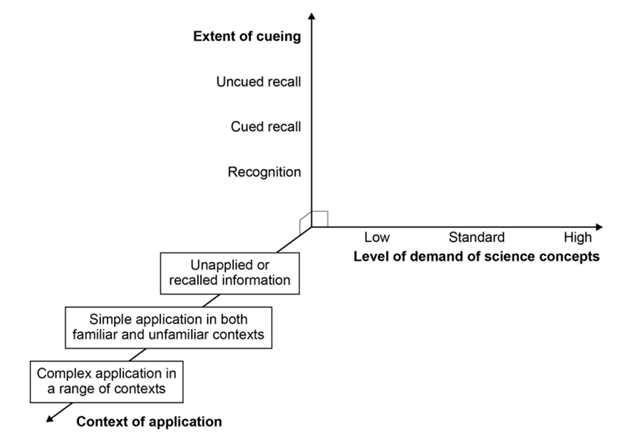
I’ll put a picture from AQA’s great document “Our exams
explained” for GCSE Science.
It encapsulates the key aspects that determine a question’s
difficulty.
(to science teachers who happen to read this post: welcome!)
(1) the difficulty of the concept you’re assessing
Not all concepts are created equal.
I’m gonna take examples from AASL so most teachers can relate.
Let’s take correlation and solving equations using
double angle formulae.
Yes, they’re both in the AASL curriculum.
Yes, they’re both pretty common on exams.
No, they’re definitely not of the same breed.
Correlation is usually considered “free marks” by most teachers
and students.
Solving equations using double angle formulae is right at
the top end of the attainment scale.
An unscientific way (I’m not aware of any evidence on this
lol) of determining a topic’s difficulty is the number of prerequisites.
Correlation requires nothing much beyond a GDC, linear graphs and a grasp of
the correlation coefficient. Trig equations, on the other hand, oh boy: exact
trig values, the trig circle, algebra (in factorising “hidden” quadratics), trig
equations and if that doesn’t scare you enough, trig identities.
(2) context of applications
This is all about the question you use to evaluate the
concept you decided above.
The context could be either
- routine – no surprises, what students have
encountered in class and/or homework exercises
- nonroutine – a twist on the routine questions they
have done, and sometimes questions they’ve never done before.
I know this categorisation can be very controversial:
a question that appears to be nonroutine to one teacher is routine to another.
Here’s a classic example.
This question is taken from Scottish National 5 Maths.
I’d be surprised if a well-prepared student hasn’t come
across anything similar to this. Sure, the first time or two the question is a little
challenging, but then it becomes part of the ever-growing bank of routine
questions.
As Adam Boxer once said in his podcast episode on Mr Barton’s
Maths Podcast: “Today’s problem solving is tomorrow’s retrieval” – without loss
of generality I’d like to rephrase this as “Today’s unfamiliar question is
tomorrow’s routine question”.
(3) level of support (cueing or scaffolding)
This is the key difference between science and maths.
For science, the extent of cueing (for theory questions) or
scaffolding (for calculations).
For maths, though, we don’t have much theory questions at
this level, so I’ll focus on the scaffolding aspect.
The two most popular forms of scaffolding are “show that”
questions and giving away the first step in the question.
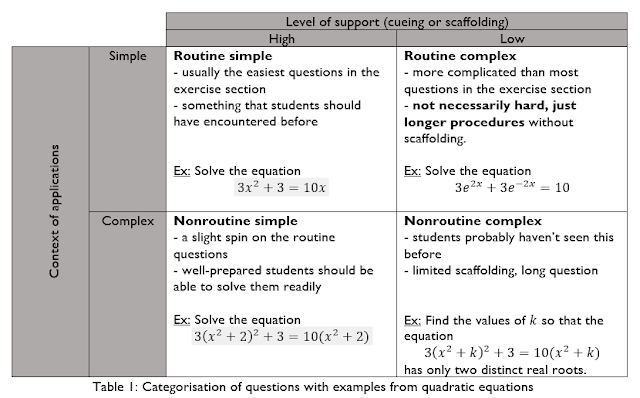
I know this could be a little overwhelming for some people,
so here’s a table for ya, with some examples from quadratic equations, which I’m
sure everyone’s familiar with.
Let me know if you have any questions, else Andrew’s out!

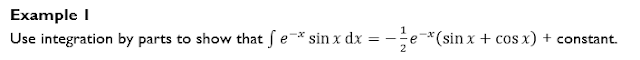

Comments
Post a Comment